(圆心O跟点A为任意点)
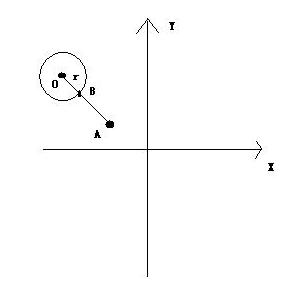
若O(x1,y1),A(x2,y2)满足OA>r。
则向量OA=(x2-x1,y2-y1),可设向量OB=(m,n),则有:m(y2-y1)-n(x2-x1)=0且(m-x1)²+(n-y1)²=r²。
解得B((x2-x1)r/√(x2-x1)²+(y2-y1)²,(y2-y1)r/√(x2-x1)²+(y2-y1)²)
圆外一点与圆心的连线与圆的两个交点
编号及代码:
/*
*Copyright(c)2015,烟台大学计算机与工程学院
*All rights reserved;
*文件名称:score.cpp
*作者:范星月
*完成日期:2015年5月28日
*版本号:v1.0
*
*问题描述:
*问题输入:定义了一个点类,一个圆类,求过圆外一点与圆心的连线与圆的交点
*问题输出:
*/
#include <iostream>
#include<cmath>
#include<iomanip>
using namespace std;
class Circle;
class Point
{
public:
Point(double a=0,double b=0):x(a),y(b) {};
friend ostream&operator<<(ostream &output,Point &p);
friend void qiujiaodian(Point &p,Circle&c,Point &p1,Point &p2);
protected:
double x,y;
};
ostream&operator<<(ostream&output,Point&p)
{
output<<"("<<p.x<<","<<p.y<<")"<<endl;
return output;
}
class Circle:public Point
{
public:
Circle(double a,double b,double r):Point(a,b),radius(r) {};
friend ostream&operator<<(ostream &output,Circle &c);
friend void qiujiaodian(Point &p,Circle&c,Point &p1,Point &p2);
private:
double radius;
};
ostream&operator<<(ostream&output,Circle &c)
{
output<<"Center=("<<c.x<<","<<c.y<<"),radius="<<c.radius<<endl;
return output;
}
void qiujiaodian(Point &p,Circle &c,Point &p1,Point &p2)
{
p1.x = (c.x + sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));
p2.x = (c.x - sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));
p1.y = (p.y + (p1.x -p.x)*(c.y-p.y)/(c.x-p.x));
p2.y = (p.y + (p2.x -p.x)*(c.y-p.y)/(c.x-p.x));
}
int main()
{
Circle c1(3,2,4);
Point p(1,1),p1,p2;
qiujiaodian(p,c1,p1,p2);
cout<<p<<endl;
cout<<c1<<endl;
cout<<"交点是:"<<endl;
cout<<setiosflags(ios::fixed)<<setprecision(2)<<endl;
cout<<p1<<endl;
cout<<p2<<endl;
return 0;
}
编号及代码:
/*
*Copyright(c)2015,烟台大学计算机与工程学院
*All rights reserved;
*文件名称:score.cpp
*作者:范星月
*完成日期:2015年5月28日
*版本号:v1.0
*
*问题描述:
*问题输入:定义了一个点类,一个圆类,求过圆外一点与圆心的连线与圆的交点
*问题输出:
*/
#include <iostream>
#include<cmath>
#include<iomanip>
using namespace std;
class Circle;
class Point
{
public:
Point(double a=0,double b=0):x(a),y(b) {};
friend ostream&operator<<(ostream &output,Point &p);
friend void qiujiaodian(Point &p,Circle&c,Point &p1,Point &p2);
protected:
double x,y;
};
ostream&operator<<(ostream&output,Point&p)
{
output<<"("<<p.x<<","<<p.y<<")"<<endl;
return output;
}
class Circle:public Point
{
public:
Circle(double a,double b,double r):Point(a,b),radius(r) {};
friend ostream&operator<<(ostream &output,Circle &c);
friend void qiujiaodian(Point &p,Circle&c,Point &p1,Point &p2);
private:
double radius;
};
ostream&operator<<(ostream&output,Circle &c)
{
output<<"Center=("<<c.x<<","<<c.y<<"),radius="<<c.radius<<endl;
return output;
}
void qiujiaodian(Point &p,Circle &c,Point &p1,Point &p2)
{
p1.x = (c.x + sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));
p2.x = (c.x - sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));
p1.y = (p.y + (p1.x -p.x)*(c.y-p.y)/(c.x-p.x));
p2.y = (p.y + (p2.x -p.x)*(c.y-p.y)/(c.x-p.x));
}
int main()
{
Circle c1(3,2,4);
Point p(1,1),p1,p2;
qiujiaodian(p,c1,p1,p2);
cout<<p<<endl;
cout<<c1<<endl;
cout<<"交点是:"<<endl;
cout<<setiosflags(ios::fixed)<<setprecision(2)<<endl;
cout<<p1<<endl;
cout<<p2<<endl;
return 0;
}